QCEngine Quick Reference

This is an active QC simulator, which provides a programming interface, as well as a programmer's visual model, for QC operations. It's not finished yet, but you're welcome to browse. Please give feedback to qc@machinelevel.com!
©2016 All rights reserved. For more information, please send email to qc@machinelevel.com

Welcome!

QCEngine is a quantum computation simulator which allows you to write code as though you had an actual working quantum computer.
This page is a programming reference, showing most of the major features, and how to use them.

Q: Where can I find samples?
A: Some simple common examples may be found here.

Q: How is this different from Microsoft's Liqui|>?
A: See this handy side-by-side overview of both: QCEngine and Liqui|>.

Q: Is QCEngine free?
A: For academic and hobby use, yes. Commercial use requires written permission.

Q: How do I get started? Where's the installation?
A: There's no installation. You can type any JavaScript program right here, and just run it.






Basic Commands and Gates

About specifying qubits: Most commands use bit masks to specify "target" or "condition" qubits. These are really just integers, where each bit in the integer (1, 2, 4, 8, 16, etc.) represents one of your qubits. Multiple qubits may be specified by simply adding them together (or else using a bitwise-or "|"). So, to specify the first and third qubits, you could use (1+4), or else (1|4), or else ((1 << 0) | (1 << 2)). If you're working with more than 32 qubits, there's a BitField data type for working with large bit masks (see below). All of this helps make QCEngine a good programmer's tool for quantum computation.

qc.reset(num_qubits); Set up a quantum simulation, with num_qubits qubits.

Note: The more qubits you ask for, the slower things will run. If you allocate too many qubits (more than about 28 or so), the actual quantum part of the simulation will shut off, and the gates will just be run in a stabilizer model, or digitally (like normal bits, not qubits).

qc.write(value_bits, target_qubits); Write the specified value to the target qubits.

var result = qc.read(target_qubits);
 Read the target qubits. This causes a measurement operation on the qubits, collapsing them and returning the result of all measured bits as a bitfield.

qc.not(target_qubits);
qc.cnot(target_qubits, condition_qubits);
 Perform a logical NOT or CNOT operation on the qubits specified by target_qubits, optionally using condition_qubits as the condition(s).

qc.hadamard(target_qubits);
qc.chadamard(target_qubits, condition_qubits); 		Perform a Hadamard operation on the qubits specified by target_qubits, optionally using condition_qubits as the condition(s).

qc.phase(theta_degrees, target_qubits); Perform a Z rotation (phase), by the specified angle.
Important note: If more than one qubit is specified, this will perform a conditional phase shift, using all specified qubits (like a CZ gate).

qc.exchange(target_qubits,
            [condition_qubits]);

 Exchange two qubits, optionally using condition_qubits as the condition(s).

qc.rotatex(theta_degrees,
           target_qubits,
           [condition_qubits]);

 Rotate in X, optionally using condition_qubits as the condition(s).

qc.rotatey(theta_degrees,
           target_qubits,
           [condition_qubits]);

 Rotate in Y, optionally using condition_qubits as the condition(s).

qc.noise(noise_level, [target_qubits]);

 Inject unitary noise, with severity (0,1]. Noise can also be added to other operations, but this allows it tp be introduced at a specific point, such as on a transmission line.

qc.postselect(one_or_zero, target_qubits);
 Read the target qubits, but force postselection to the desired value if possible. The value should be 0 or 1, and all bits will try to match it.

qc.codeLabel('my label'); Label the code. This draws a handy visual label in the gates view, and can also be used to re-run a specific set of gates, using qc.runLabel('my label').

var prob = qc.peekQubitProbability(target_qubit);
 Return the probability [0,1] that the target qubit will return 1 if read.
Note: This is handy in simulation, but it won't work on a real quantum computer. Also, it can be slow.

var cplx_val = qc.peekComplexValue(value);
qc.pokeComplexValue(value, real, imag);
 Get or set a single value in the state vector.
Note: This is handy in simulation, but it won't work on a real quantum computer. Also, it can be slow.


QInt: Quantum Integers

This is a simple and powerful mechanism for writing quantum computation code. Essentially, it allows you to group qubits into logical integers, assign them to JavaScript variables, arrays, whatever you like, and then perform operations on them.

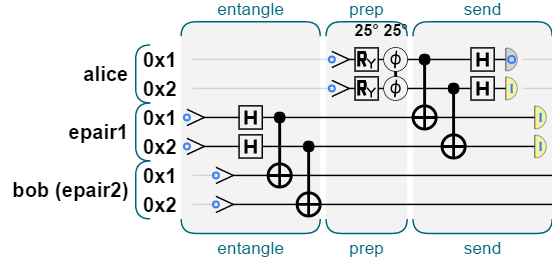
Using qints is spiffy because:
  • You can treat them as regular JavaScript variables.
  • They'll be automatically labelled in the gate view, as shown in this teleportation example:
  • Best of all, by simply increasing the number of bits in the qint, the exact same code can scale up to handle more complex cases:

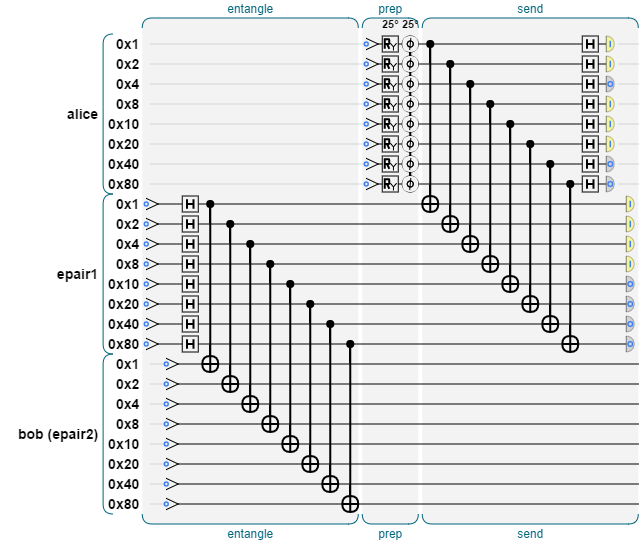
    ...this will be important as quantum computers begin to scale up in complexity.
var my_qint = qint.new(num_qubits, name); Allocate a quantum integer from your existing qubits. If you've run out of qublts, this will return null.

my_qint.not([target_qubits]);
 Perform a logical NOT operation on the qint's qubits specified by target_qubits.

my_qint.cnot(condition_qint, [target_qubits]);


 Perform a bit-by-bit logical CNOT operation between two qints, optionally specifying target_qubits.

my_qint.hadamard([target_qubits]);
my_qint.chadamard(condition_qint, [target_qubits]);

 Perform a Hadamard operation optionally bitwise conditional on another qint, and optionally specifying target_qubits.

my_qint.exchange(condition_qint, [target_qubits]);

 Exchange two qints, optionally specifying target_qubits.

my_qint.write(value, [mask]);

 Write a value to the qint, optionally masked to certain qubits. This is performed by reading the value, and then executing a NOT on any bits which need to change.

var result = my_qint.read([mask]);
var result = my_qint.readSigned([mask]);

 Read the qint, optionally masked to certain qubits, and return the result.
readSigned() returns the number as a signed value.
my_qint.add(other_int_or_qint, [condition_qubits]);
my_qint.subtract(other_int_or_qint, [condition_qubits]);
 Add (or subtract) an integer, or another qint, to this one. This is equivalent to the += operator, optionally conditional on condition_qubits.

my_qint.addSquared(other_int_or_qint, [condition_qubits]);
my_qint.subtractSquared(other_int_or_qint, [condition_qubits]);
 Add (or subtract) the square of an integer, or another qint, to this one.
This is equivalent to a += b * b, optionally conditional on condition_qubits.

my_qint.rollLeft(shift, [condition_qubits]); Perform a logical roll-left (which is a bit-shift with wrap-around).
This is equivalent to a multiplication by 2 (if the top bit is zero), optionally conditional on condition_qubits.

my_qint.negate(); Multiply this qint by -1.

my_qint.reverseBits([condition_qubits]);
 Reverse the bit order of this int, optionally conditional on condition_qubits.

my_qint.addSquared(other_int_or_qint, [condition_qubits]);
my_qint.subtractSquared(other_int_or_qint, [condition_qubits]);
 Add (or subtract) the square of an integer, or another qint, to this one.
This is equivalent to a+=b*b, optionally conditional on condition_qubits.

my_qint.QFT();
my_qint.invQFT();

 Perform a QFT (or inverse QFT) operation on this qint.

my_qint.Grover([condition_qubits]);
 Perform a Grover iteration (reflection about the mean), optionally conditional on condition_qubits.

var bf = my_qint.bits([bit_mask]);
 Return a bitfield representing the qc bits used by this qint, optionally masked out.
Note: This allocates a new BitField, so you'll get better performance if you call bf.recycle(); on it when you're done, rather than depending on garbage collection.

var prob = my_qint.peekProbability(value);
 Return the probability [0,1] that this qint will read the specific value provided.
Note: This is handy in simulation, but it won't work on a real quantum computer. Also, it can be slow.

var val = my_qint.peekHighestProbability(value);
 Return the integer value most likely to be returned by a call to read().
Note: This is handy in simulation, but it won't work on a real quantum computer. Also, it can be slow.


BitFields

(documentation coming soon)
...
 ...


Stabilizer Simulation

The stabilizer sim is based on CHP, by Scott Aaronson.
It's useful for running a limited set of gates on very large numbers of qubits. To see specific examples of use, look here.

You can switch back and forth between simulators, even within the same program, in order to use the right tool for the right job:


qc.start_chp_sim()
 Start using the CHP stabilizer simulation, instead of the normal state vector simulation.

qc.stop_chp_sim()
 Stop using the CHP stabilizer simulation, and transfer the state back to the normal state vector sim.


Linear Optics Simulation

The linear optics simulation allows operations using beam splitters (such as fusion gates and postselected optical CNOT gates) which don't map to qubits.

The first version of this was adapted from lojs, by Pete Shadbolt.
To see specific examples of use, look here.

You can switch back and forth between simulators, even within the same program, which is really very handy:


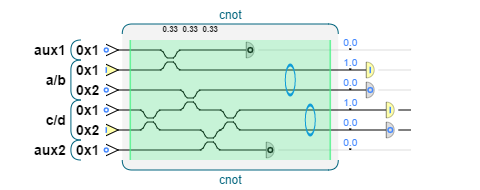
qc.start_photon_sim()
 Start using the linear optical simulation, instead of the normal state vector simulation.

qc.stop_photon_sim()
 Stop using the linear optical simulation, and transfer the state back to the normal state vector sim.

qc.dual_rail_beamsplitter(reflectivity, target_qubits)


 Perform a beamsplitter operation with quantum interference and the selected reflectivity.

qc.postselect_qubit(target_qubits)


 Perform postselection, requiring exactly one of the two rails to be 1, if possible.

qc.polarization_grating_in(target_qubits, input_side)
qc.polarization_grating_out(target_qubits, input_side)
 Convert a polarized qubit into a position-encoded qubit, or back. The input_side parameter should be 1 or -1; this determines which qubit to pull from or push to.




Documentation is being added as time permits, but if you'd like more info on something, just send me a note at the email address above!